1706. 球会落何处¶
难度:中等
题目¶
用一个大小为 m x n 的二维网格 grid 表示一个箱子。你有 n 颗球。箱子的顶部和底部都是开着的。
箱子中的每个单元格都有一个对角线挡板,跨过单元格的两个角,可以将球导向左侧或者右侧。
- 将球导向右侧的挡板跨过左上角和右下角,在网格中用
1表示。 - 将球导向左侧的挡板跨过右上角和左下角,在网格中用
-1表示。
在箱子每一列的顶端各放一颗球。每颗球都可能卡在箱子里或从底部掉出来。如果球恰好卡在两块挡板之间的 "V" 形图案,或者被一块挡导向到箱子的任意一侧边上,就会卡住。
返回一个大小为 n 的数组 answer ,其中 answer[i] 是球放在顶部的第 i 列后从底部掉出来的那一列对应的下标,如果球卡在盒子里,则返回 -1 。
示例 1:
输入:
grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]]输出:
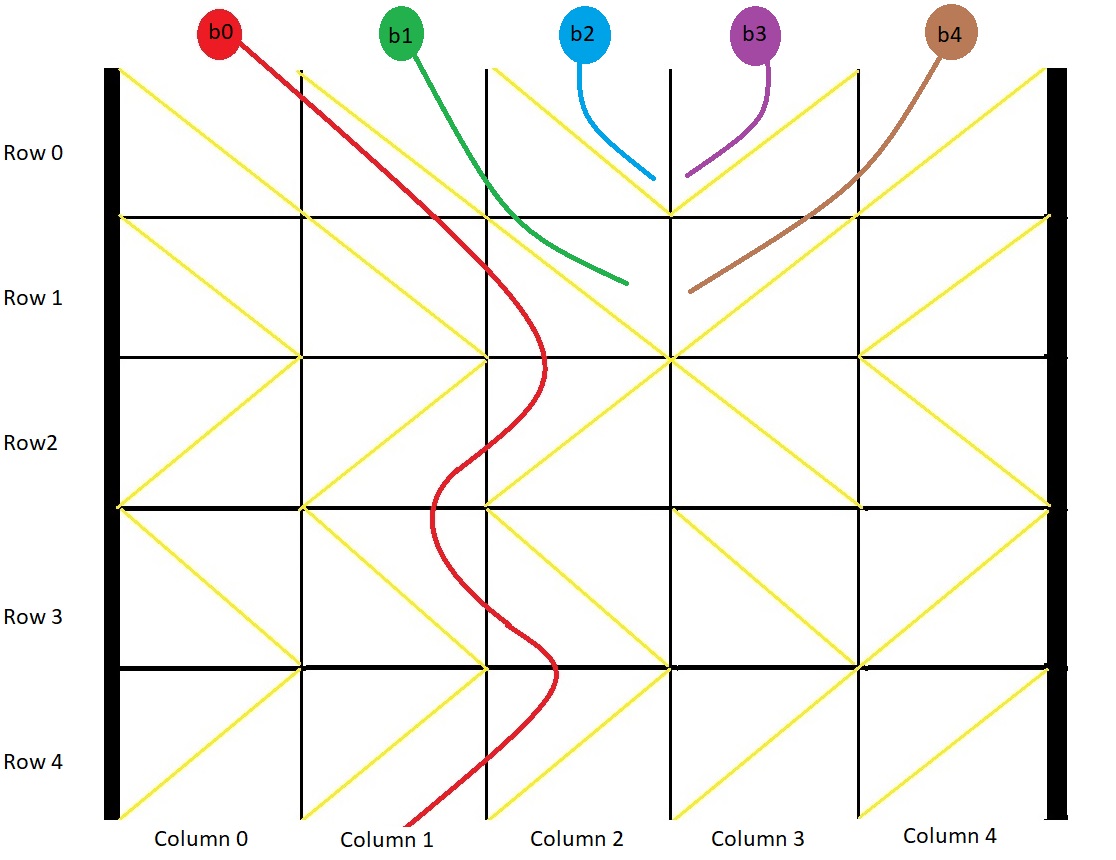
[1,-1,-1,-1,-1]解释:示例如图:
b0 球开始放在第 0 列上,最终从箱子底部第 1 列掉出。
b1 球开始放在第 1 列上,会卡在第 2、3 列和第 1 行之间的 "V" 形里。
b2 球开始放在第 2 列上,会卡在第 2、3 列和第 0 行之间的 "V" 形里。
b3 球开始放在第 3 列上,会卡在第 2、3 列和第 0 行之间的 "V" 形里。
b4 球开始放在第 4 列上,会卡在第 2、3 列和第 1 行之间的 "V" 形里。
示例 2:
输入:
grid = [[-1]]输出:
[-1]解释:球被卡在箱子左侧边上。
示例 3:
输入:
grid = [[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1],[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1]]输出:
[0,1,2,3,4,-1]
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 100grid[i][j]为1或-1
题解¶
逐列模拟小球的行为,当小球处于i行j列位置时,小球下一次所在的列为j + grid[i][j]。当出现以下条件时,小球不能移动:
j + grid[i][j]小于0或大于等于len(grid[0])(总列数),此时小球会被边界卡住。grid[i][j]和grid[i][j + grid[i][j]]符号不同,此时说明隔板构成一个V型凹槽卡住小球。
当以上两个条件都通过时,小球可以向下移动到i + 1行j + grid[i][j]列处,重复以上过程直到小球离开盒子或小球卡住。
class Solution:
def simulate(self, grid: List[List[int]], currentCol: int) -> int:
currentRow, height, width = 0, len(grid), len(grid[0])
while currentRow < height:
nextCol = currentCol + grid[currentRow][currentCol]
if nextCol < 0 or nextCol >= width:
return -1
if grid[currentRow][currentCol] != grid[currentRow][nextCol]:
return -1
currentRow += 1
currentCol = nextCol
return currentCol
def findBall(self, grid: List[List[int]]) -> List[int]:
return [
self.simulate(grid, i)
for i in range(len(grid[0]))
]