2218. 从栈中取出 K 个硬币的最大面值和¶

难度：困难

题目¶

一张桌子上总共有 n 个硬币栈。每个栈有 正整数 个带面值的硬币。

每一次操作中，你可以从任意一个栈的顶部取出 1 个硬币，从栈中移除它，并放入你的钱包里。

给你一个列表 piles ，其中 piles[i] 是一个整数数组，分别表示第 i 个栈里 从顶到底 的硬币面值。同时给你一个正整数 k ，请你返回在恰好进行 k 次操作的前提下，你钱包里硬币面值之和 最大为多少 。

示例 1：

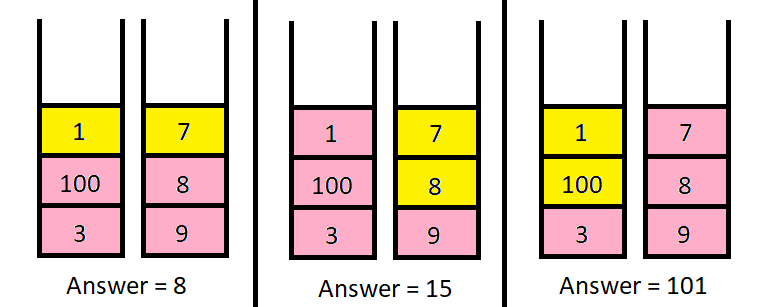
输入：piles = [[1,100,3],[7,8,9]], k = 2

输出：101

解释：

上图展示了几种选择 k 个硬币的不同方法。

我们可以得到的最大面值为 101 。

示例 2：

输入：piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7

输出：706

解释：

如果我们所有硬币都从最后一个栈中取，可以得到最大面值和。

提示：

n == piles.length
1 <= n <= 1000
1 <= piles[i][j] <= 10^5
1 <= k <= sum(piles[i].length) <= 2000

Reference

题解¶

从前i + 1个栈中取出j个元素的最大面值和可以分解为从第i + 1个栈中取出k个硬币，剩余j - k个硬币从前i个栈中按照最优（最大）的方式取出。取出的方式有如下可能：

从第i + 1个栈中取出0个硬币，从剩余i个栈中取出j个硬币
从第i + 1个栈中取出1个硬币，从剩余i个栈中取出j - 1个硬币
...
从第i + 1个栈中取出j个硬币，从剩余i个栈中取出0个硬币

遍历每个栈，使用一个表dp[j]存储在第i次遍历中，从前i个列表中取出恰好j个硬币的最大面值和。那么，根据取出方式，下一轮次的dp[j]为如下所述各种取出方式的最大值。

从第i + 1个栈中取出0个硬币，从剩余i个栈中取出j个硬币，最大面值为dp[j]
从第i + 1个栈中取出1个硬币，从剩余i个栈中取出j - 1个硬币，最大面值为dp[j - 1] + sum(piles[i][:1])
...
从第i + 1个栈中取出j个硬币，从剩余i个栈中取出0个硬币，最大面值为dp[0] + sum(piles[i][:j])

在初始状态时，dp的值为第一个栈的面值前缀和，dp[0] = 0对应不取出硬币的情况。每轮迭代更新dp，最后一轮更新后，dp[k]即为所求。

class Solution:
    def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:
        dp = [0, *itertools.accumulate(piles[0])][:k + 1]
        num_piles, step = len(piles), 1
        while step < num_piles:
            dp_length, pile_length, new_choices = len(dp), len(piles[step]), []
            cum = [0, *itertools.accumulate(piles[step])]
            for total in range(k + 1):
                max_value = 0
                for right in range(min(pile_length, total), -1, -1):
                    left = total - right
                    if left >= dp_length:
                        break

                    max_value = max(max_value, dp[left] + cum[right])
                new_choices.append(max_value)
            dp = new_choices[:k + 1]
            step += 1

        return dp[-1]

2218. 从栈中取出 K 个硬币的最大面值和¶

题目¶

题解¶

评论