2920. 收集所有金币可获得的最大积分¶

难度：困难

题目¶

有一棵由 n 个节点组成的无向树，以 0 为根节点，节点编号从 0 到 n - 1 。给你一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [a_i, b_i] 表示在树上的节点 a_i 和 b_i 之间存在一条边。另给你一个下标从 0 开始、长度为 n 的数组 coins 和一个整数 k ，其中 coins[i] 表示节点 i 处的金币数量。

从根节点开始，你必须收集所有金币。要想收集节点上的金币，必须先收集该节点的祖先节点上的金币。

节点 i 上的金币可以用下述方法之一进行收集：

收集所有金币，得到共计 coins[i] - k 点积分。如果 coins[i] - k 是负数，你将会失去 abs(coins[i] - k) 点积分。
收集所有金币，得到共计 floor(coins[i] / 2) 点积分。如果采用这种方法，节点 i 子树中所有节点 j 的金币数 coins[j] 将会减少至 floor(coins[j] / 2) 。

返回收集所有树节点的金币之后可以获得的最大积分。

示例 1：

输入：edges = [[0,1],[1,2],[2,3]], coins = [10,10,3,3], k = 5

输出：11

解释：

使用第一种方法收集节点 0 上的所有金币。总积分 = 10 - 5 = 5 。

使用第一种方法收集节点 1 上的所有金币。总积分 = 5 + (10 - 5) = 10 。

使用第二种方法收集节点 2 上的所有金币。所以节点 3 上的金币将会变为 floor(3 / 2) = 1 ，总积分 = 10 + floor(3 / 2) = 11 。

使用第二种方法收集节点 3 上的所有金币。总积分 = 11 + floor(1 / 2) = 11.

可以证明收集所有节点上的金币能获得的最大积分是 11 。

示例 2：

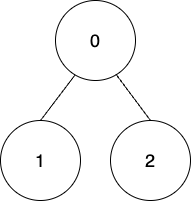
输入：edges = [[0,1],[0,2]], coins = [8,4,4], k = 0

输出：16

解释：

使用第一种方法收集所有节点上的金币，因此，总积分 = (8 - 0) + (4 - 0) + (4 - 0) = 16 。

提示：

n == coins.length
2 <= n <= 10^5
0 <= coins[i] <= 10^4
edges.length == n - 1
0 <= edges[i][0], edges[i][1] < n
0 <= k <= 10^4

Reference

题解¶

使用一个表dp[node][t]存储节点node在其父节点执行t次操作2后，所能获得的最大积分。

使用第一种方法，当前节点获得的积分为(coins[node] >> t) - k，之后收集子节点获得的积分为sum(dp[_][t] for _ in child)
使用第二种方法，当前节点获得的积分为(coins[node] >> t + 1)，之后收集子节点获得的积分为sum(dp[_][t + 1] for _ in child)

之后反向层序遍历树，从叶子节点开始，逐步计算收集节点获得的积分，最终dp[0][0]即位所求的积分值。注意coins[node] <= 10^4，而\(2^13 = 8192 < 10^4, 2^14 = 16384 > 10^4\)，因此对于\(t \geq 14\)的情况，收集子节点获得的积分固定为\(0\)，可以借此限制dp表的宽度。

另外，edges列表并没有保证第一个元素是父节点，第二个元素是子节点，需要手动处理。

class Solution:
    def maximumPoints(self, edges: List[List[int]], coins: List[int], k: int) -> int:
        node_order, descs = [{0}], {i: set() for i, _ in enumerate(coins)}

        # Parse tree
        for a, b in edges:
            descs[a].add(b)
            descs[b].add(a)
        parent_layer = set()

        while True:
            # Layer iteration
            new_layer, current_layer = set(), node_order[-1]
            for node in current_layer:
                descs[node] -= parent_layer
                new_layer |= descs[node]

            if not new_layer:
                break
            parent_layer = current_layer
            node_order.append(new_layer)

        # dp[node][times]
        dp: List[List[int]] = [[0] * 14 for _ in coins]

        for level in node_order[::-1]:
            for node in level:
                child = descs[node]
                for t in range(14):
                    # Method 1:
                    result1 = (coins[node] >> t) - k + sum(dp[_][t] for _ in child)
                    # Method 2:
                    result2 = (coins[node] >> t + 1)
                    if t < 13:
                        result2 += sum(dp[_][t + 1] for _ in child)
                    dp[node][t] = max(result1, result2)

        return dp[0][0]

2920. 收集所有金币可获得的最大积分¶

题目¶

题解¶

评论